Printed Circuit Board

In a printed circuit board, conductive wires are laid on a non-conductive board. Because the conductors in the same layer cannot cross without creating short-circuits, boards with conductors divided into several layers separated by non-conductive board material are used in more complex cases. However, boards with more layers are more expensive. So, manufacturers try to allocate the required conductors to layers in a way that minimizes the number of layers needed.

In this task we look at boards where each conductor is connecting two ports located on opposite edges of the board and seek to minimize the cost of such a board.

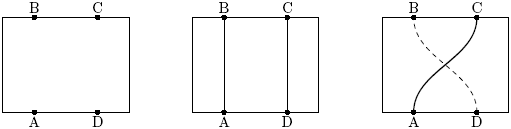
Consider, for example, the board shown on the left on the figure below. If one conductor has to connect A to B and another D to C, this could be achieved in a single layer, as shown in the middle on the figure. But a conductor connecting A to C and another connecting D to B could not be laid out in the same layer, as can be seen on the right on the figure.

Write a program that is given the locations of the endpoints of the N conductors on a WxH board and determines the minimal number of layers needed to accommodate all of them.

It may be assumed the width of the conductors is very small compared to the distances between the ports. That is, between any two conductors, there is always enough room for a third one.

Input Data

The first line of the text file pcb.in contains N (1 ≤ N ≤ 10⁵), the number of connectors. Each of the following N lines contains two integers, X_i1 and X_i2 (0 ≤ X_ij ≤ 10⁶), separated by a space, meaning that the i-th conductor has to connect the points (X_i1,0) and (X_i2,H). It may be assumed that all the 2N endpoints given in the input are distinct.

Output Data

The first and only line of the text file pcb.out should contain a single integer, the minimal number of layers needed to accommodate all the required conductors.

Examples